INTRODUCTION
As part of a project I am working on, I was required to estimate the speed of the person walking while holding a tablet in his hands. The person will be holding the tablet right in front of him, looking at the screen as he walks. I initially considered looking at the absolute accelerometer value and integrate that to get velocity. But accelerometer technology is far from perfected. The integrated velocity value will be way off within just a few seconds of moving the device around.
So we scrapped that idea, and decided instead to use a step counting algorithm to determine user velocity. We use the accelerometer to calculate when the user takes each step, and using that, estimate the velocity (assuming each step is a fixed length). This is certainly very approximate. But one thing it does fairly well is detect changes in speeds of walking, even if the absolute speed value might not be.
The algorithm that I came up with for step detection is based on finding maxima in the acceleration values. I came up with it largely by experimentation, so it works fairly well for this specific case.
So we scrapped that idea, and decided instead to use a step counting algorithm to determine user velocity. We use the accelerometer to calculate when the user takes each step, and using that, estimate the velocity (assuming each step is a fixed length). This is certainly very approximate. But one thing it does fairly well is detect changes in speeds of walking, even if the absolute speed value might not be.
The algorithm that I came up with for step detection is based on finding maxima in the acceleration values. I came up with it largely by experimentation, so it works fairly well for this specific case.
THE GOAL
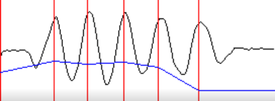
This is a graph generated by my program by shaking it up and down a few times. There's going to be many of these, so I might as well explain it now. There are three pieces to this graph -
It's important to note that the black acceleration line has already been significantly smoothed using a smoothing window. If you have ever seen acceleration values coming off of a smartphone accelerometer, you know that the raw signal is far noisier.
- The smoothed out acceleration values from the accelerometer (Black)
- The time points when a maxima was detected (Red lines)
- The calculated velocity (Blue)
It's important to note that the black acceleration line has already been significantly smoothed using a smoothing window. If you have ever seen acceleration values coming off of a smartphone accelerometer, you know that the raw signal is far noisier.
THE PROBLEM
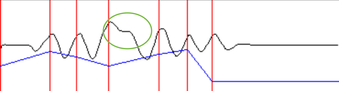
Since this app will actually be used in the real world by people who don't care about how all of this works, the actual acceleration patterns aren't going to be as ideal as in the case above. So it's not possible to just look for a decreasing slope and then take that point to be a maxima. There can be situations like this:
Look at the area in the green oval. The acceleration doesn't really start back up before it goes down again. This was probably caused by a jerk of the hand while walking with the tablet. We need to make sure that is not considered in our step calculations.
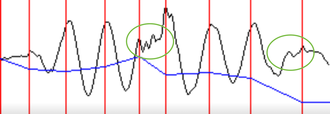
Here's another worse situation:
Here's another worse situation:
Look at the acceleration patterns inside the green ovals. Those tiny peaks are basically noise, but a basic maxima-finding algorithm will pick all of it up as steps!
So how do we eliminate such noise? Well, what you want to do is to really think about it's characteristics. What makes the noise signals different from the actual step signals? There are a few differentiating factors:
- The noise signals are usually much smaller, and are higher frequency.
- They don't always have the shape of a maxima (the inverted U shape).
What I ended up doing was use a bunch of different techniques to eliminate different problems.
For each acceleration value received, I check the following:
There was still a problem though. For some reason, I got bands of maxima at each peak. Turns out that near the top of the peak, a number of acceleration values satisfy the required conditions. So I just replaced bands of maxima with the first one. Whenever a new maxima is detected, I look at how far behind the previous maxima is. If it is really close, I disregard this one.
Another important point to mention here - You might have realized that this won't work because I am looking at acceleration values ahead of the one in consideration, but if I am checking the newest acceleration value, then I don't know what the next few values are going to be! I solve this by adding the newest acceleration value to the list of accelerations, but checking for a maxima with the acceleration value from a few time-steps behind. This causes a small delay in the step finding, but for the most part, it works without a problem.
For each acceleration value received, I check the following:
- Check if the slope of the line formed by connecting the previous and next acceleration value is nearly 0.
- Check if the average of a few points behind and in front of the acceleration value is significantly below the current acceleration.
- Check if the maxima occurred below the 0 acceleration line (ie. Check if the acceleration was negative when the maxima was detected)
There was still a problem though. For some reason, I got bands of maxima at each peak. Turns out that near the top of the peak, a number of acceleration values satisfy the required conditions. So I just replaced bands of maxima with the first one. Whenever a new maxima is detected, I look at how far behind the previous maxima is. If it is really close, I disregard this one.
Another important point to mention here - You might have realized that this won't work because I am looking at acceleration values ahead of the one in consideration, but if I am checking the newest acceleration value, then I don't know what the next few values are going to be! I solve this by adding the newest acceleration value to the list of accelerations, but checking for a maxima with the acceleration value from a few time-steps behind. This causes a small delay in the step finding, but for the most part, it works without a problem.
CALCULATING VELOCITY
Now that we know when each step is being taken, we can work backwards to estimate how fast the user is moving. For this, we assume (rather arbitrarily) that the user moves forward 1 meter with each step. This is of course different for different people. One way of improving the estimate might be to ask for users' heights and provide a better step length estimation based on that. But the actual velocity is less important for the app I'm making so I'd rather not have to make users type in their height to use it.
Now since each step covers 1m. The speed is then 1m/time between the previous step and that step. This is what is being shown by the blue velocity line in the above graphs. It works surprisingly well!
Now since each step covers 1m. The speed is then 1m/time between the previous step and that step. This is what is being shown by the blue velocity line in the above graphs. It works surprisingly well!
MORE FEATURES
There are some more techniques you can add to improve the step counting even further. One of them is Adaptive Thresholding. So instead of defining constant thresholds and tuning them based on the specific use case, you can use a function to calculate a good threshold based on previous acceleration values and use that instead. This allows for fairly good step tracking when the mobile device is in arbitrarily changing positions and rotations.
Here's a great paper on one way to do this
Here's a great paper on one way to do this